Posted in: Aha! Blog > Eureka Math Blog > Conceptual Understanding > How far is the moon?
Imagine staring up at the moon on a spring evening and wondering, “how far away is the moon?” What would you do to figure out how far away it is? Perhaps take out your smart phone to Google it? How is it then that the Greeks, who posed the same question 2,200 years ago, found the answer without the aid of Google, NASA, or any modern technology? The Greeks were able to determine a reasonably accurate distance from the earth to the moon using careful observations, measurements, and a clever geometric model of the situation. In the Eureka curriculum, when presented with this same question,“students would use modeling or mathematical pictures — Eureka uses a short list of such flexible models throughout its 14 grades — to bridge the gap between the word problem and the abstract operations needed for the right answer" (Center for Digital Education).
IDENTIFYING KEY INFORMATION
The Greek astronomer and mathematician, Aristarchus of Samos, calculated the distance from the earth to the moon with only the following information:
- The earth’s diameter was approximately 8,000 miles (another ingenious calculation, made by Eratosthenes).
- Experimentation showed that in order to block out the sun with a spherical object, the ratio of the length of the object’s shadow to the object’s diameter must be 108:1. For example, a one-inch marble can just block out the sun at 108 inches from the eye. If it were any further, the marble would appear smaller than the sun and a ring of light would be visible around the marble. If the marble were any closer than 108 inches, it would completely block out the sun. This phenomenon is true regardless of the size of the obstructing object and is also true in order to block out the moon, which has the same apparent size in the sky as the sun. It can be concluded, then, that the moon is 108 moon diameters away from the earth since it just blocks out the sun during a solar eclipse.
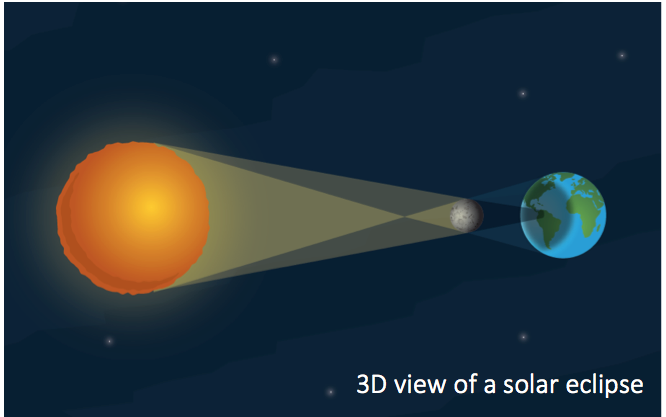
- Shadows cast by planetary bodies are conical in shape and are assumed to be similar. In a two dimensional view, then, the shadows cast by the moon and the earth are similar isosceles triangles:
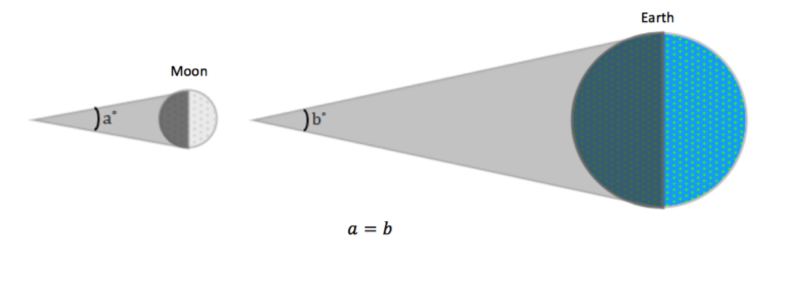
The next piece of information was a result of close observation of lunar eclipses.
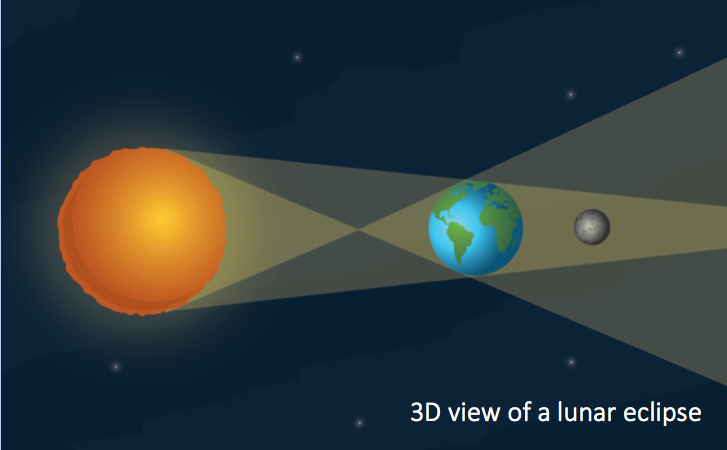
- During a total eclipse, it was observed that the moon traveled a distance equal to two and one half moon diameters while passing through the earth’s shadow. Check out an animation of the moon passing through the earth’s shadow HERE.
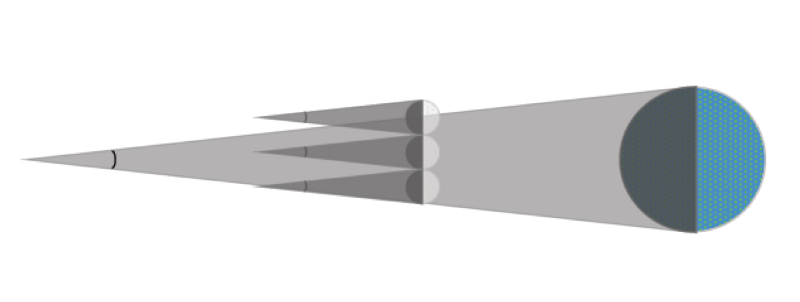
FORMULATING A MODEL
With these pieces of information, a model was developed. In this model, the moon and its shadow is reversed so that one side of the shadow aligned with one side of the earth’s shadow and is positioned so that the moon’s shadow tapered just as it reached the earth. Let the moon diameter be equal to 1 unit. Then AF is 1 unit, and FD must be 2.5 units, as determined by the lunar eclipse observations.
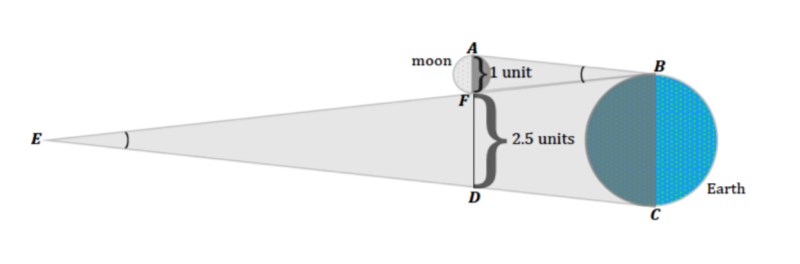


We have now established that the diameter of the moon, AF, has a length of approximately 2,300 miles. AB is 108 times this length. Then, based on the information we began with, the distance between the earth and the moon is (2,300 x 108) miles, or approximately 248,000 miles.
Modern-day calculations show that the distance from the earth to the moon varies between 225,622 miles and 252,088 miles due to the Earth’s orbit being elliptical versus circular. Still, Aristarchus managed to make an incredible estimation, considering the tools he had at his disposal and the magnitude of the distances he was working with.
For any problem, whether it involves values of great magnitude as in this problem, or a more humble problem involving a number of cookies, a model allows us to make sense of what we are investigating by assigning a concrete visual or system to otherwise abstract mathematical manipulation. “Familiarity with a few powerful models breeds comfort in learning mathematics.”
This post is by Pia Mohsen, a former teacher, who is a Grade 10 writer for the Eureka Math curriculum.
© Great Minds 2016
Submit the Form to Print

Pia Mohsen
Pia graduated from the University of Pennsylvania with a Bachelor of Arts in Economics and a minor in Psychology. She taught high school math at the New York Harbor School for seven years through the New York City Teaching Fellows program. After moving to Philadelphia, she joined the Eureka Math team and helped write the first edition of Geometry for the curriculum. Outside of work, Pia enjoys getting crafty by making cards and finding new corners of Philadelphia to explore with her husband and two boys.
Topics: Conceptual Understanding




.jpg?width=430&name=PhD%20Science%20(1).jpg)




.jpg?width=430&name=EurekaMath%20(1).jpg)
.jpg?width=430&name=WitWisdom%20(1).jpg)

