Fractional Division Interpretation: What is the Difference Between “Partitive” and “Measurement”?

Recently during a national mathematics conference, I posed the question, “How many of us understand the difference between partitive and measurement division?” Out of the 165 participants in the room, only two participants raised their hand. This lead me to think that somehow this information isn’t as widely understood as I initially thought, or hoped. Let’s begin with understanding missing factors and how they relate to division interpretation.

Missing Factors:

A student’s ability to set a path to solve division problems with real-world contexts lies heavily in understanding what has often been referred to as the “missing factor” approach. Starting with this approach, students can intuitively decide which interpretation of division is most efficient when applying to real-world contexts. Let’s take a look at 24÷6 as a solution to the following:

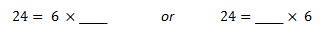
The first interpretation asks, “24 is 6 groups, or parts, of what number, or size?” Since we know the original amount, and the number of parts, it is the size of the parts that is missing. Hence, we use partitive division to determine the size of the parts that is missing. The diagram below shows this rationale.

Note that the diagram is divided equally into the 6 known parts.

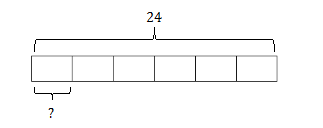
The second interpretation asks, “24 is how many groups, or parts, of 6?” Here we know the original amount and the size (or measure) of each of the parts. What is missing is the number of parts. We use measurement division to determine the missing number of parts. The diagram below shows this rationale.

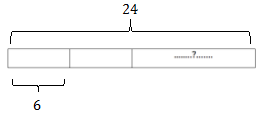
Note that we can label the known measure of each part, but we must figure out how many parts of this known measure there are in 24.

Measurement Interpretation and How it Relates to Division of Fractions:

Savannah has 1/2 yard of fabric to make placemats for her dining room table. She needs 1/8 yard of fabric for each placemat. How many placemats will Savannah make with 1/2 yard of fabric?

The underlying division expression associated with this context is 1/2 ÷ 1/8. We can look at this from the measurement interpretation of division. We can ask ourselves, “1/2 is how many groups, or parts, of 1/8?” or more simply, “How many 1/8 are there in 1/2? We can model this with a diagram:

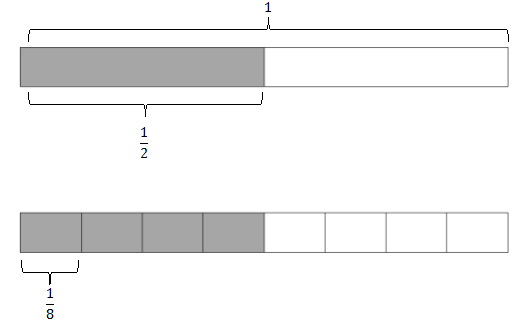
It is clear from the diagram that there are 4 parts, or equal groups, of 1/8 in 1/2. Hence, Savannah will be able to make 4 placemats. Sometimes the context of the problem with the same division expression calls for a different approach.

Partitive Interpretation and How it Relates to Division of Fractions:

Savannah is making curtains for her dining room and has 1/2 yard of fabric. According to the craft store clerk, this is only 1/8 the amount of fabric she needs. How many yards of fabric will Savannah need to make the curtains?

The underlying division expression associated with this context is, again, 1/2 ÷ 1/8. We can look at this from the partitive interpretation of division. Since we know the original amount, we can ask ourselves, “1/2 is 1/8 group of what size?” or more simply, “1/2 is 1/8 of what size?” We can model this with a diagram:

Note that there are eight equal parts and one of those groups is labeled 1/2.

We can rely on unit form to determine the size. We know that 1 unit out of 8 is equal to 1/2. We also know that we need to know how many 8 units are.

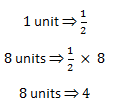
What is opportune about partitive division is the direct connection to the invert and multiply rule. Can you see during the partitive process where the invert and multiply rule appears? Let’s take a closer look.

Partitive Interpretation and How it Relates to Division of Fractions and the Invert and Multiply Rule: 

We, as educators, in the past have always told our students to “Keep, Change, Flip” when dividing fractions. Students keep the dividend the same, change the operation of division to multiplication and then flip the divisor. Since the process was never explained, this “trick” is mostly meaningless to students. Students who are fluent with partitive division can intuitively notice the direct connection between partitive interpretation of division and the invert and multiply rule. Out of context, let’s look at and evaluate the expression 3/4 ÷ 2/3. We can begin by asking ourselves, “3/4 is 2/3 of what size?” Note the diagram below that will assist us in making the connection between partitive division and the invert and multiply rule. We see that the diagram is divided equally into three parts. Two of those parts are labeled with the original amount, 3/4. We can use these two parts to find the value of all three parts, or the missing size.

Again, we can rely on unit form to determine the size. We know that 2 units out of 3 is equal to 3/4. We also know that we need to know how many 3 units are. Let’s start by figuring out the value of one unit. 

What can we conclude from this development?

This blog post was written by Erika Silva a Eureka Math writer for grades 6–8.