If figures are what we study in mathematics, then transformations are how we relate them. Transformations are significant to the Eureka Math Geometry curriculum and to the Common Core State Standards (CCSS), both of which approach transformations in a more purposeful way than before. What distinguishes how they were formerly studied versus how they are being studied now?
A look into most textbooks predating the CCSS reveals this distinction. Even by casual observation, there was heavy, if not constant, use of the coordinate plane in the chapter on transformations. A student would have seen rotations performed by a convenient 90, 180, or 270 degrees. Reflections were applied across the x or y axis and across the y = x or y = -x lines.
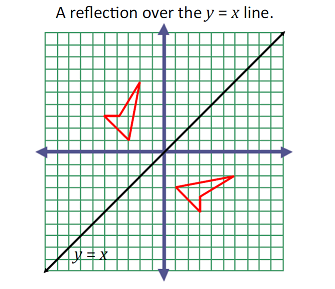
A set of specific transformations was previously studied so that each transformation in the set neatly mapped to easy-to-manage coordinates. A student might have gotten the impression that only a fixed number of possible transformations existed! In reality, transformations that map to not-so-easy-to-manage coordinates do exist: a reflection can be performed over any line, a rotation or a dilation can be performed about any point, and a translation can be performed along any vector.
This broader perspective makes transformations abundant in the plane, as there are endless lines, points, and vectors to select from. Eureka Math introduces students to this flexibility with transformations before examining transformations in the coordinate plane, which do not enjoy the same kind of abundance.
Previously, the topic on transformations was treated as an isolated topic; a study of the transformations chapter had no impact on any other chapter in a textbook. Now, the way transformations are taught gives students the ability to manipulate figures in the plane freely, which sets the foundation for other areas of study, such as the verification of perpendicular segments, the derivation of the equation of a circle, and perhaps most notably, congruence and similarity.
This post is by Pia Mohsen, a former teacher, who is a Grade 10 writer for the Eureka Math curriculum.
Pia Mohsen
Pia graduated from the University of Pennsylvania with a Bachelor of Arts in Economics and a minor in Psychology. She taught high school math at the New York Harbor School for seven years through the New York City Teaching Fellows program. After moving to Philadelphia, she joined the Eureka Math team and helped write the first edition of Geometry for the curriculum. Outside of work, Pia enjoys getting crafty by making cards and finding new corners of Philadelphia to explore with her husband and two boys.
Topics: Conceptual Understanding
Get the Latest Great Minds Updates
Stay informed of simple yet crucial implementation support tips, curriculum updates, new resources, professional development opportunities, and more for math, science, and ELA.
.jpg)
.jpg)
.jpg)
