The Number Bond: A K-5 Model That Fosters Number Sense

AHA! MOMENT

In math education, the term “number sense” is thrown around all the time, ad nauseam. We all want our students to have it, as it’s often juxtaposed with rote memorization. But what does number sense really mean? Number sense is making sense of the part-whole relationships between quantities, working flexibly with numbers, using strategies and properties of operations to solve (e.g., the associative property), and understanding that a problem can be approached in multiple ways.

So, how do we teach number sense?

There are a few things that have changed my life: getting married, having children, the number bond. No joke. This simple model encourages students to reason about quantities, to look closely, and to think. From Kindergarten through 5th Grade, the number bond has opened my eyes to the multiple, often creative, ways that we can solve problems and share solution strategies. If you are new to the number bond model, this K-5 coherent strand is for you.

Grade K

In Kindergarten (Module 4) decomposition and composition are taught simultaneously using the number bond model so students begin to understand the relationship between parts and wholes. They begin to see that the numbers 6 through 10 can be “friendly” as students find smaller quantities embedded within them, e.g., 1 and 5 embedded within 6 (see below).

There are 6 apples in a bowl. 1 apple is yellow. 5 apples are green.

This work is foundational to fluency in Grade 1 with sums and differences to 10, as well as fluency with sums and differences to 20 in Grade 2.

Grade 1

Grade 1 students learn to complete a unit of ten, as exemplified below. Students use familiar 5-group drawings from kindergarten as a pictorial scaffold for the increasingly complex numerical number bond representation.

Once students can make a “ten”, they can easily make “the next ten,” or 60, as shown above with the problem 59+6=60+5. This empowers them to complete a unit of a hundred in Grade 2.

Grade 2

A Grade 2 student sees that just as 9 or 59 is close to the “ten” or “next ten”, so is 390 only 10 away from the next hundred, in this case, 400 (shown below).

Can we use the number bond for subtraction? Absolutely. Grade 1 students solve simple subtraction problems via the “take from ten” strategy. Grade 2 students then extend this understanding to “taking from a hundred” to make a simpler problem (shown below).

In the Grade 2 example above, notice how close 198 is to the next hundred, 200. Students need not subtract via renaming with the traditional algorithm. Instead, they can use the number bond and their understanding of part-whole relationships to create a simpler problem.

Grade 3

In Grade 3, students continue to use the number bond, now adding new units to their repertoire. Students see that just as we can add and subtract ones, tens, and hundreds, we can also add and subtract twos, threes, fourths, fifths, etc. Let’s look at parallel below:

Notice how the decomposition of 6 apples as 1 yellow apple and 5 green apples in Kindergarten sets the stage for the distributive property in Grade 3 when the unit changes from ones to nines: 6 nines = 1 nine + 5 nines.

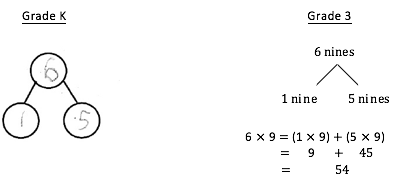
Why do we bother teaching students to decompose multiplication facts using the number bond model? In Eureka Math, students consistently use what they know, rather than learning “tricks”, to help them solve more challenging problems. We know that multiplying by nines can be challenging for our students, but multiplying by fives is a simpler, more manageable task. So here, we can break apart 6 nines into 2 smaller parts, 1 nine and 5 nines.

Grade 3 students also begin work with the essential building blocks of fractions, namely unit fractions, e.g., 1/2, 1/3, 1/4, 1/5, etc. They see that any fraction can be decomposed into smaller unit fractions. Below, you can see how students decompose 5/5 into 5 units of 1/5. Then, students can break apart 6 fifths, such that 6/5 = 5/5 + 1/5.

Grade 4

In Grade 4, students see that they can manipulate fractions to complete simple arithmetic, adding and subtracting with like units. So, just as the Grade 1 student can complete “1 ten,” the Grade 4 student can complete “1 one.” 

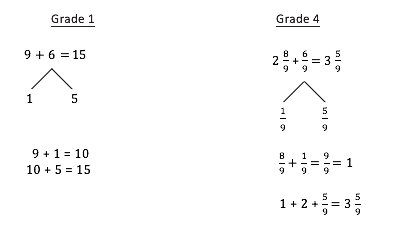
The Grade 4 student understands that 8 ninths is close to 1 one (9 ninths). The Grade 4 student decomposes 6 ninths such that 6/9 = 1/9 + 5/9. Then, he/she combines 8/9 and 1/9 first to make 1 one. The remaining parts are combined to make 3 5/9.

Grade 4 students can also use their understanding of decomposing a unit (i.e., recall taking from a ten or a hundred) to take from the one (shown below).

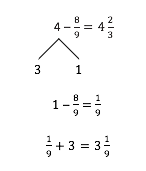
Grade 5

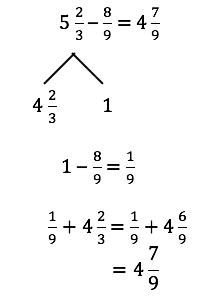
In Grade 5, the new complexity arises when students face units that are not equivalent. Now, students must create equivalent units in order to successfully add or subtract. As illustrated in the problem below, students find a like unit, which is a multiple of both denominators. Here, the largest like unit is ninths. Students multiply both the numerator and the denominator by 3 to rename 2/3 as a number of ninths.

Grade 5 students also use the number bond to decompose fractions to take from the one. Here, the Grade 5 student decomposes 5 2/3 to subtract 8/9 from 1 one, or 9/9. Now, the student works through a simpler addition problem, 1/9 + 4 2/3, changing thirds for smaller equal units, e.g., ninths, that can then be added.

Conclusion

The number bond is one of a number of coherent models that students regularly use in A Story of Units. For me, it supports the number sense that many adults are lacking, because we were children of the memorization generation. Seeing part-whole relationships and multiple solution paths and is an important component of number sense. A student may know that 7 x 6 = 42, because 7 sixes = 5 sixes + 2 sixes, thus applying the earlier understanding that 7 = 5 + 2. The number bond is a powerful model that supports what we all want for our students: the ability to think flexibly, strategically, and creatively. Your students will thank you later.